モンティ・ホール問題…これなら小学生でもわかる！

はじめて「モンティ・ホール問題」を目にしたのが2003年になりますので、かれこれ15年かかって、やっと疑問が解決しました。

もちろん、15年間ずっと考えているほどひまではありませんので、4〜5年の周期で少し考えては納得できない…ということを繰り返していました。

実は、解決したのも今さっきで、「モンティ・ホール問題は納得できない」というタイトルで記事を書こうとしていました。

しかし、とあることを思いついたら、あっさり解決してしまいました。

きっと、これなら今まで納得できなかった方も、「わかった」となると思います。

「モンティ・ホール問題」をおさらいしよう

 

モンティ・ホールが司会者を務めるアメリカのゲームショー番組で行われたゲームに関する論争。

ショーの中の一幕なので、そのあたりの心理的な影響も微妙に絡んでおり、問題が複雑になってしまっているようです。

ちなみに、答えとしては、選んだドアを変更したほうが、変更しない方よりも2倍程度景品をゲットしているというプログラムによるシミュレーション結果が出ています。

 

どうしても理解できない人の考え方

まるで、他人事のようにかいていますが、過去の自分自信の考え方ですので、披露します。

３つあるどのドアも、当然景品が入っている確率は、すべて同じで1/3。

プレイヤーが１つ選んだ後で、モンティがひとつハズレドアを開いた場合、残りの2つのドアに景品が入っている確率は、その段階で同じ1/2になる。

だから、選び直そうが、そのままにしても、それぞれのドアに景品が入っている確率は1/2である。

 

設定に振り回されるからこじれる

この問題を、「各ドアの景品が入っている確率」としてしまうと間違えのもとになります。

また、ショーであるため余計な演出があり、答えを導くのを邪魔しています。

 

ドアを100枚にして考えることで、見えてくる？

100枚のドアを使う方法で極端な表現にすることで、わかりやすくしているのですが、「各ドアの景品が入っている確率」と考えれば、同じになってしまいます。

 

超シンプルにしたら解決

問題の定義があいまいなので、整理します。

ここでは、選んだ「ドアの中に景品が入っている確率」として考えてしまう人と、「プレイヤーが景品をゲット出来る確率」と考える人がいるでしょう。

この違いが答えを変えてしまっています。

ここでは、「プレーヤーはドアを変更すべきだろうか？」と聞いていますので「プレイヤーが景品をゲット出来る確率」と考える必要があります。

ちなみに、理解出来ない人は、「ドアの中に景品が入っている確率」と考えていると思います。

 

全てをそぎ落として考えたら、あっさり解決。

３つのドアから１つのドアをプレイヤーが選びます。

このドアを第一グループ（赤枠）とします（1つのドアで1グループ＝景品がある確率は1/3）。

残りの２つのドアを第2グループ（黄枠）とします（2つのドアで1グループ＝景品がある確率は2/3）。

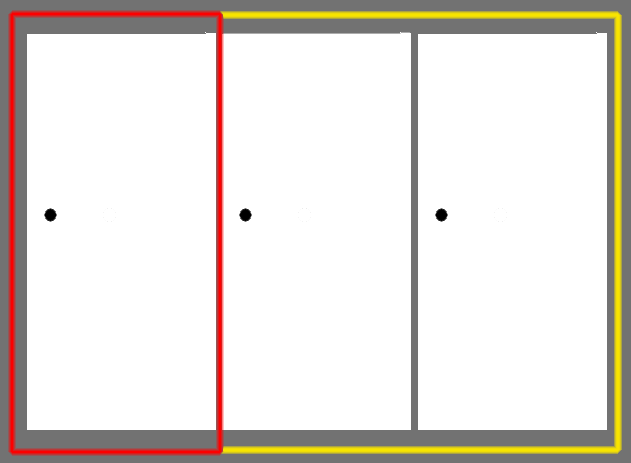
ここで、モンティが第2グループの１つのハズレドアを開きますが、実は開けなくても同じです（ルール上、第2グループのハズレを選ぶので）。

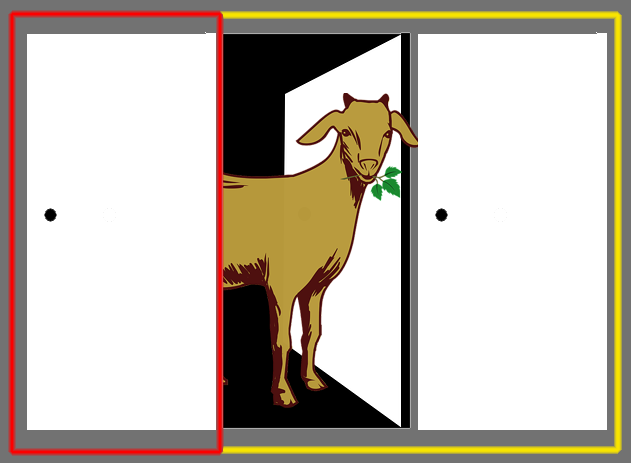
ドアを開けることによって、グループではなくドア単体に見えてしまいます。

つまり、ドアを選びなおすのではなく、第1グループと第2グループを選び直してもいいと言っているのです（100枚のドアなら、第2グループは99枚のドアになります）。

 

こう考えてみよう

プレイヤーが最初に選んだ１つのドアの第１グループと、２つのドアの第２グループのどちらを選べば、景品をゲットできる確率が上がるかということです。

ハズレドアを開くのは、演出ですので、開こうが開くまいが、ドアを選び直すということは、2枚のドアの第2グループを選択出来るということになります。

だから、約2倍の確率で景品をゲットできるというプログラムによるシミュレーション結果と同じになるということです。

 

まとめ

モンティ・ホール問題は、アメリカのゲームショー番組で行われたゲームに関する論争。

この問題をわかりにくくしているのは、ショーの要素です。

• 「ドアの中に景品が入っている確率」
• 「プレイヤーが景品をゲット出来る確率」

この違いが答えを変えてしまっています。

問題では「プレイヤーはドアを変更すべきだろうか？」と聞いています。

よって「プレイヤーが景品をゲット出来る確率」と考える必要があります。

モンティはハズレドアを開けますが、開ける必要はありません（考える上で開けないで考えます）。

ドアを開けるので、迷うのです。

最初に選んだ1つのドアのグループか、残りの2つのドアのあるグループに変更するかということと同義です。

2枚のドアのグループを選び直せば、景品の確率は2倍になります。